摘要 提高凸轮的加工质量是目前弧面分度凸轮研究的一个重点。但无论是其静态几何量测量,还是加工误差分析,首先要解决的是凸轮理论轮廓面的计算。本文在对弧面分度凸轮轮廓面详尽分析的基础上,论述了弧面分度凸轮理论轮廓面的计算及以 Visual C ++ 5.0 开发的面向凸轮加工精度分析的理论轮廓面计算软件包。该软件包可应用于凸轮 CAD 、 CAM 、 CAQ 等子系统。
1 引言
弧面凸轮分度机构被评价为目前最理想的高速精密分度机构。我国对弧面分度凸轮的研究始于 70 年代末,少数厂家已具备小批量生产该凸轮机构的能力。但从总体上看,要提高我国的弧面分度凸轮机构的制造能力,还有许多方面的工作要做。如设计和开发标准化系列产品,以求更大范围地满足国内外市场的需求;开发优化实用的 CAD/CAM 系统,以期缩短设计周期,提高设计效率;研究切实可行的检测原理和方法,以便检验和指导制造;加强机构的动力学分析及研究,最终使该机构的性能得以充分地发挥,等等。
本文在现有研究成果的基础上,以开发面向凸轮加工精度分析系统为目标,研究了弧面分度凸轮理论轮廓面的计算,开发了弧面分度凸轮理论轮廓面计算的软件包。该软件包以 Visual C++5.0 为开发工具,具有面向对象技术软件的继承性和封装性,界面友好,可应用于凸轮 CAD 、 CAM 、 CAQ 等子系统。 7
2 凸轮轮廓面方程
2.1 弧面分度凸轮轮廓面特征
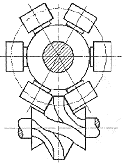
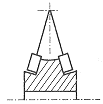
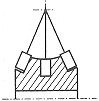
弧面分度凸轮机构 ( 见图 1a) 类似弧面蜗杆传动,凸轮为凹圆弧回转体,与蜗杆一样可制成单头、双头或多头,且凸脊的旋向也与蜗杆旋向定义相同,分为左旋和右旋。凸轮以其定位段形式的差异,又分为 A 型 ( 图 1b) 和 B 型 (1c) 两种结构类型, A 型定位段是凸脊,有两个滚子跨夹于凸脊上, B 型定位段是凹槽,有一个滚子在定位段槽中。此外,无论哪种结构的凸轮,其凸脊均有左右两个侧面。根据不同的旋向一侧为受力侧,推动分度盘转动,另一侧为几何定位侧,局部区域与滚子之间可以有一定间隙。
(a) (b) (c)
图 1 弧面分度凸轮轮廓面特征
(a) 机构简图 (b)A 型结构 (c)B 型结构
不同于蜗杆的是,凸轮的轮廓为变升程的螺旋带,其加工需要专用数控机床,属高技术产品。加工时,刀具相当于分度盘上的滚子,机床只需控制刀具的中心轨迹按照分度盘相对于凸轮的运动规律转动即可。但由于凸轮的轮廓面为一复杂的不可展空间曲面,目前对其廓面质量的最佳检测手段就是运用三坐标测量机,因此,凸轮轮廓面坐标及廓面法向量的计算便成为质量保证体系首要解决的问题。
2.2 轮廓面方程的建立
弧面分度凸轮的轮廓面方程,在已有文献中存在多种表面形式 [ 1 ~ 4 ] 。为便于与通用设计、制造形式相统一,适于三坐标测量,本文采用常规符号,在考虑测量坐标系的前提下,对轮廓面方程的建立如下:
如图 1a 所示机构形式,其坐标系建立见图 2 。定义动坐标系 S f ( O f - X f Y f Z f )与分度盘固结,动坐标系 S c ( O c - X c Y c Z c )与凸轮固结;定义参考坐标系,即定坐标系 S 1 ( O 1 - X 1 Y 1 Z 1 ),其 Z 轴与分度盘 Z 轴重合,称为分度盘参考坐标系,定坐标系 S 2 ( O 2 - X 2 Y 2 Z 2 )的 Z 轴与凸轮 Z 轴重合,称为凸轮参考坐标系。凸轮以 ω 2 匀速转动,按右手定则,其旋向为正。分度盘以变角速度 ω 1 转动,同样按右手定则,左旋凸轮 ω 1 为正,右旋凸轮 ω 1 为负。 |
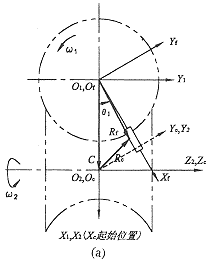 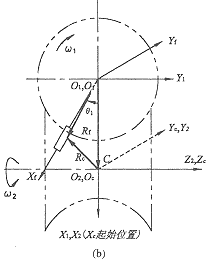
图 2 轮廓面方程的建立
(a) 左旋凸轮 (b) 右旋凸轮
机构基本结构尺寸:中心距 C ,滚子半径 r f ,分度盘回转半径 l f ,凸轮头数 n ,分度角 θ h ,滚子数 z ,分度盘转位角 θ d , θ d = 2 nπ / z 。
以 A 型左旋凸轮为例,设凸轮以 ω 2 转过 θ 2 ,分度盘以 ω 1 转过 θ 1 ,滚子上高度为 δ f 的点矢量为 R f ( X f , Y f , Z f )。根据空间啮合原理:两曲面在共轭点处重合并相切,其相对速度垂直于该点的公法线,可推得啮合线方程。再将啮合线上的点 ( 共轭点 ) R f 在 S f 坐标系的坐标转换到 S c 坐标系中,即可得到弧面分度凸轮轮廓面方程: 8
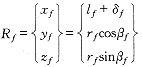 ( 1 ) ( 1 )
以 Z 1 为轴, S f 坐标系顺时针旋转 θ 1 角,得 R f 在 S 1 坐标系中的坐标:
R 1 = E Z 1 θ 1 R f ( 2 )
S 1 平移 C ( C , 0 , 0) ,再以 X 2 为轴, S 1 坐标系顺时针旋转 90° 角,得 R 1 在 S 2 坐标系中的坐标:
R 2 = E X 2 ( 90° ) ( R 1 - C ) ( 3 )
以 Z 2 为轴, S 2 坐标系逆时针旋转 θ 2 角,得 R 2 在 S c 坐标系中的坐标:
R c = E Z 2 (- θ 2 ) R 2 ( 4 )
以上变换表达为:
R C = E Z 2 (- θ 2 ) E X 2 ( 90° ) ( E Z 1 θ 1 R f - C ) ( 5 )
其中:
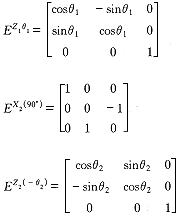
将式 (1) 代入式 (5) ,得
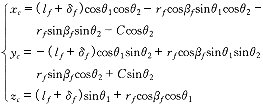 ( 6 ) ( 6 )
对于右旋凸轮, ω 2 方向不变, ω 1 沿反向 — 顺向时针方向转动,则
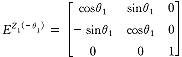
同理,可得右旋凸轮廓面方程。加入符号变量 F ={ 1 ,- 1 },( 1 为左旋, -1 为右旋 ) ,轮廓面方程表示为:
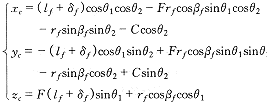 ( 7 ) ( 7 )
其啮合线方程仍以左旋推导,共轭矢量 R f 及 R c 分别在 S 1 、 S 2 坐标系中的矢量为 R 1 、 R 2 ,对其求一阶导数得其速度:
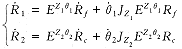 ( 8 ) ( 8 )
R 1 与 R 2 在啮合点的相对滑动速度表示在坐标系 S 1 中,得
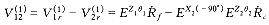 ( 9 ) ( 9 )
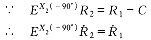 ( 10 ) ( 10 )
将式 (8) 代入式 (10) ,得
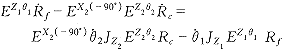
对比式 (9) ,得
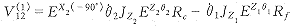 ( 11 ) ( 11 )
在 S f 坐标系中
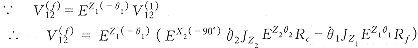 ( 12 ) ( 12 )
将式 (5) 代入式 (12) ,得
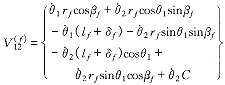 ( 13 ) ( 13 )
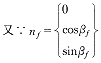
根据空间啮合原理 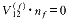
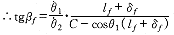 ( 14 ) ( 14 )
同理,可得右旋凸轮啮合线方程。加入符号变量 F ={ 1 , 1 },啮合线方程表示为:
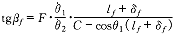 ( 15 ) ( 15 )
2.3 法向量值
由于通常曲面的外法线方向规定为正向,所以轮廓面的法向量可由
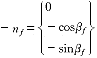
经坐标变换得到:
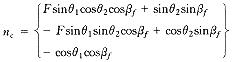 ( 16 ) ( 16 )
3 从动件运动规律的计算
3.1 简谐梯形运动规律通式
从动件运动规律在分度运动段多选用修正正弦、修正梯形等简谐梯形组合运动规律。其兼有简谐运动规律在两端连续及梯形运动规律最大加速度低的优点。且可以通过优化手段,得到满足特定要求的优化通用凸轮运动曲线。其运动规律的位移曲线通式为:
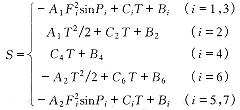 ( 17 ) ( 17 )
简谐梯形运动规律通式的应用,参见文献[ 6 ]。软件收录了常用的 16 种运动曲线,且可随时添加新的运动曲线。
3.2 从动件运动规律
凸轮轮廓面计算的关键是计算每一凸轮转角 θ 2 对应的从动件角位移 θ 1 和角速度 ω 1 。 θ 2 - θ 1 见图 4 。图示为一个凸轮回转周期从动盘的角位移曲线。该曲线分为起始段、停歇 Ⅰ 段、分度段、停歇 Ⅱ 段和结束段。通常凸轮为对称的,其 α = β 。在非停歇段,曲线对应分度运动段运动规律 —— 简谐梯形运动规律,该曲线表示为 f s ( T )= s × θ d 。各段曲线计算公式见下表。对 B 型凸轮,其 θ 1 只需在现有值上加 θ d / 2 即可。
表
段落名称 |
区间宽度 |
θ 2 |
T( 无因次时间 ) |
θ 1 |
起始段 |
s α |
[-( α + γ + θ h /2 ),-( γ + θ h /2 )] |
[( θ h - α ) / θ h , 1 ] |
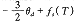
|
停歇 Ⅰ 段 |
γ = 360° - θ h |
[-( γ + θ h /2 ),- θ h /2 ] |
|
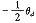
|
分度段 |
θ h |
[ θ h /2 ,- θ h /2 ] |
[ 0 , 1 ] |
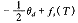
|
停歇 Ⅱ 段 |
γ = 360° - θ h |
[ θ h /2 ,( γ + θ h /2 )] |
|
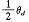
|
结束段 |
β |
[ γ + θ h /2 , γ + θ h /2 + β ] |
[ 0 , β / θ h ] |
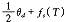
|
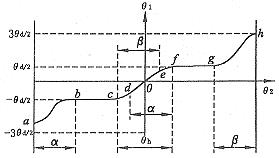
图 3 θ 1 - θ 2 关系图
4 程序实现
弧面分度凸轮轮廓面的计算程序是以 VisualC++5.0 为工具开发的。轮廓面计算软件的功能模块组成见图 4 。该程序被 CAD / CAM 系统利用,如运动规律选择功能。但主要功能是用于凸轮的检测及加工精度分析。
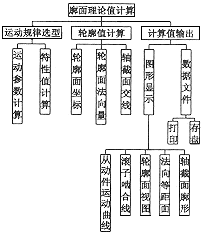
图 4 程序功能模块
程序核心类及其成员函数组成有:运动曲线类 (Ccurve) 为基类,成员函数有 calculateA,calculateV,calculateS,calculateJ; 派生类为弧面凸轮从动件运动规律类 (Cfollow) 其成员函数有 calculateTht1,calculateThtV1,calculateBeta,calculatePrfl, 等等。程序界面及运行结果示例如图 5 所示。
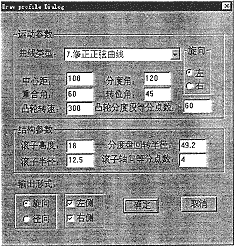 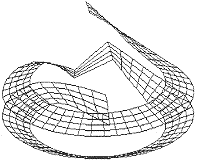
(a) 绘轮廓图对话框 (b) 轮廓面啮合线框图
图 5 运行实例
5 结束语
正确便捷地计算理论轮廓面值,是弧面分度凸轮检测和误差分析的关键环节。在建立适于加工和测量的轮廓面方程的基础上开发的轮廓面计算软件,其操作简便,界面友好,可计算任一侧面按任意网格密度化分的轮廓面离散点,并以图形和数据文件形式输出。现已在廓面检测及分析工作中应用,证明该程序正确、可靠且实用。 |





